Excelについて詳しく解説します
- 中央値と平均値との使い分けについて知りたい
- Excelで中央値を計算する関数をわかりやすく教えて欲しい
- 平均値を使ったグラフの活用方法なども知りたい!
当記事では、上記のような疑問にお答えします。
中央値は平均値とは違い、外れ値を除外しつつ実態に近い値を表せます。
使い方によっては非常に便利です。
しかし、Excelで中央値を出すにはどうすればいいのか?
そもそも、いつ使うのか?がわかりませんよね。
そこで当記事では、Excelで中央値を出す方法や使い方、グラフで中央値を表現する方法を解説します。
この記事を読めば、中央値の使い方やExcelでの表現方法がわかるので、ぜひ1度読んでみてください。
目次
そもそも中央値とは
中央値は、データ全体の傾向を表す代表値の1つです。
あるデータ範囲内の値を小さい順(昇順)か大きい順(降順)で並べたときに、ちょうど真ん中に来る値が中央値となります。
たとえば、「4,1,7,2,9」と5つのデータがあったとしましょう。
データを小さい順に並べ替えると「1,2,4,7,9」となるので、4が中央値となります。
もしデータの総数が偶数であれば、真ん中にある2つの値を足して2で割った数値が中央値です。
これも例をあげると「3,1,5,8,6,9」とデータがあった場合、小さい順に並べ替えると「1,3,5,6,8,9」になります。
真ん中にあるのは5と6なので、足して2で割った5.5が中央値です。
中央値を使う場面(平均値との使い分け)
中央値はデータ範囲内にある異常値を取り除きたい場合に、使いましょう。
平均値とは違いデータ内の極端に低い数値や高い数値の影響を受けないため、実態に近い数値となります。
下記画像のように、平均値が中央値とかなり差があったら相手に誤解を与える可能性があります。
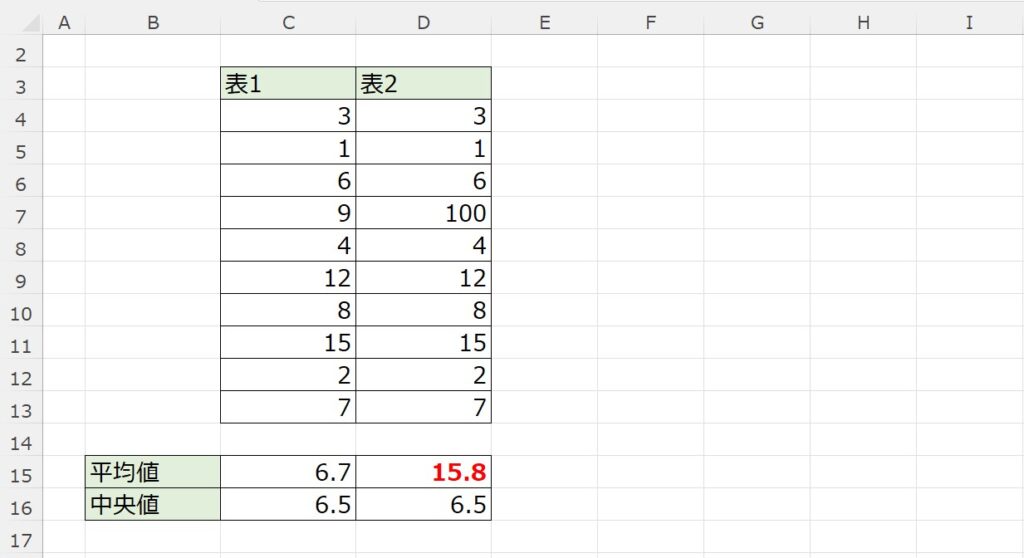
実態に近い数値で相手を説得したい場合に、中央値を使うのがいいでしょう。
中央値を求めるMEDIAN関数の使い方
Excelで中央値を出すには、MEDIAN関数を使います。
中央値を出すには以下のステップがあります。
- データの総数を計算して並び替える
- 総数が奇数か偶数かを判断する
- 偶数であれば真ん中にある2つの値を足して2で割る
データ総数が10個くらいであれば自力で中央値を算出できそうですが、100個以上だとすぐに算出するのは大変です。
しかし、MEDIAN関数を使えば一瞬で中央値を算出できます。
MEDIAN関数の書き方は
です。
実際に使ってみましょう。
以下に2つの表を作成しました。
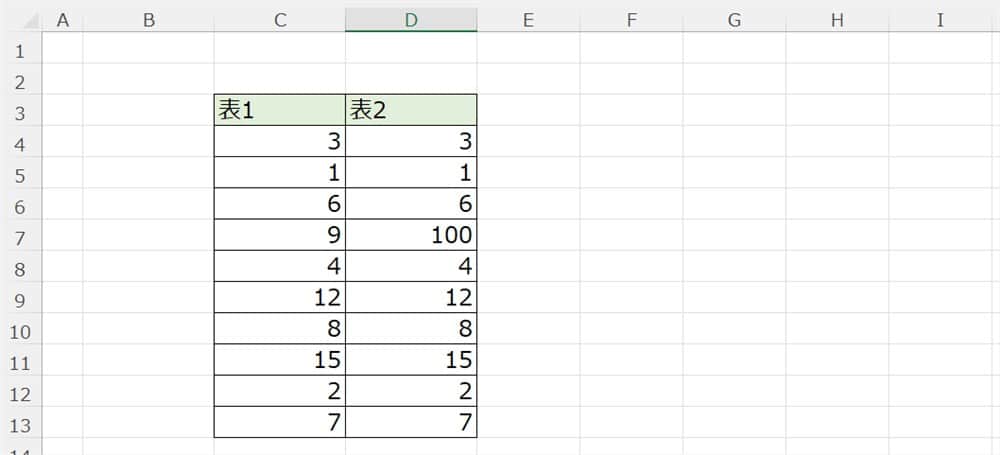
左側の表は平均値から外れていない数値を入れ、もう1つは極端に高い数値をあえて入れました。
この2つの表の平均値と中央値を出してみましょう。
表1の中央値は、
で、表2の中央値は
と入力します。
平均値はAVERAGE関数で出しましょう。
すると、下記のようになります。
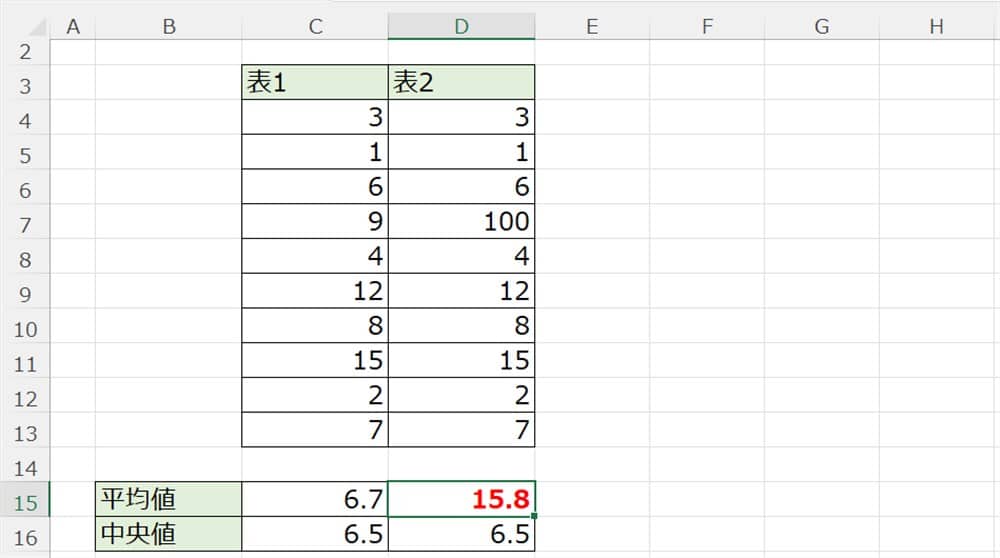
1つは中央値と差異のない平均値が算出されましたが、もう1つは中央値とはかなりかけ離れた平均値となりました。
中央値が異常値の影響を受けていないのがわかります。
【応用①】ifを使って特定条件下のセルの中央値を求める
状況によっては条件付きで中央値を算出場合があるかもしれません。
条件付きの中央値を出す場合、
で特定条件下の中央値を算出できます。
条件を2つ以上入れたい場合は、IFを入れ子にして入力します。
たとえば、以下のテストの成績表で学年別・教科別の中央値を出したいとしましょう。
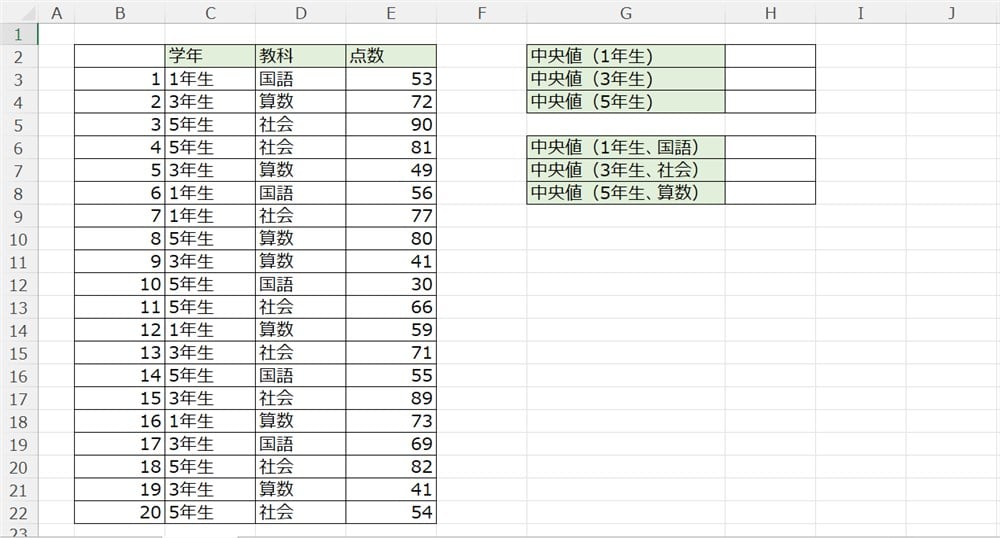
それぞれのパターンについて解説します。
単一の条件で中央値を出す
まずは、学年ごとの中央値を出してみましょう。
1年生であれば、
と、入力します。
すると、下記画像のようになります。
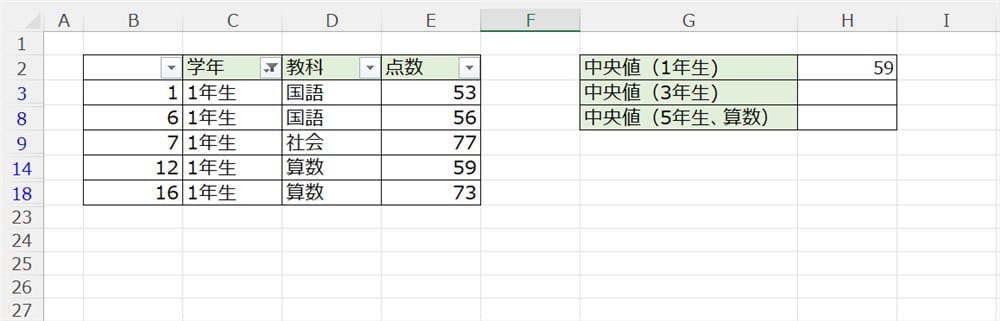
念のためフィルターをかけて、確認してみました。
1年生だけの中央値が算出できています。
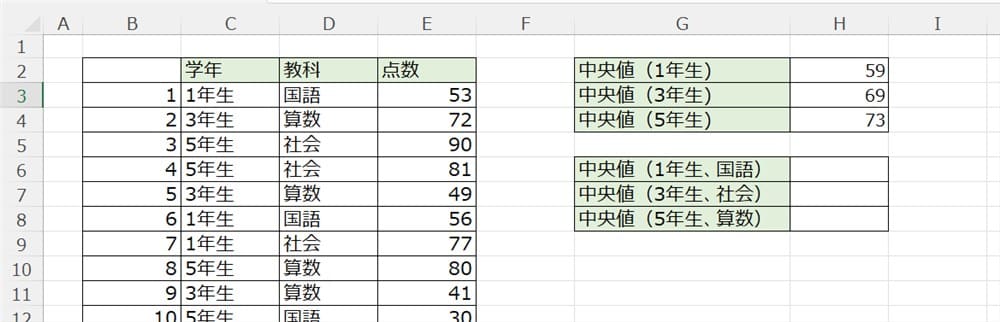
同様に、3年生も5年生も出してみました。
すると下記のようになります。
複数条件で中央値を出す
今度は複数条件で中央値を出してみます。
1年生の国語の中央値を出してみましょう。
下記のように入力してください。
すると、下記のようになります。
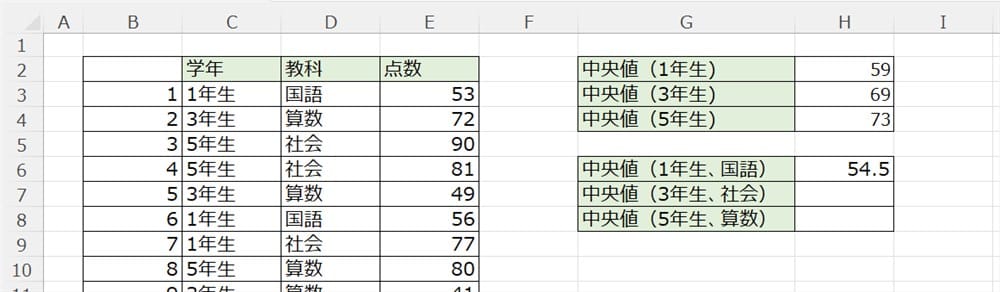
同様に他の中央値も出してみます。
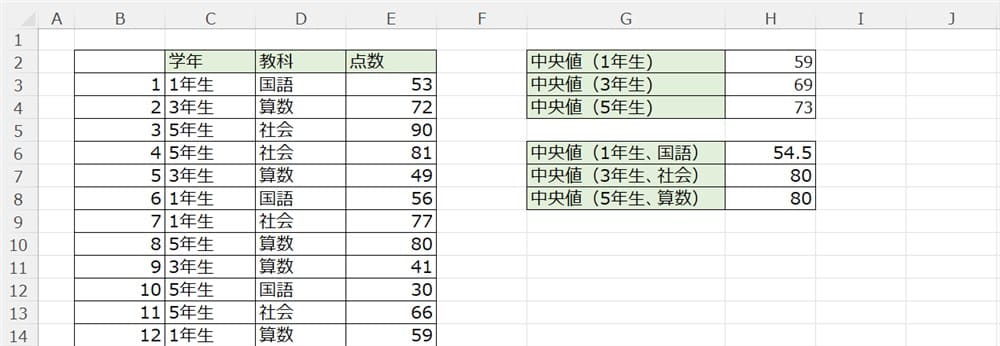
条件付きで中央値を出す方法も覚えておくと便利です。
【応用②】中央値を使ってグラフを強調する
棒グラフや折れ線グラフに中央値を入れてグラフを強調するのもオススメです。
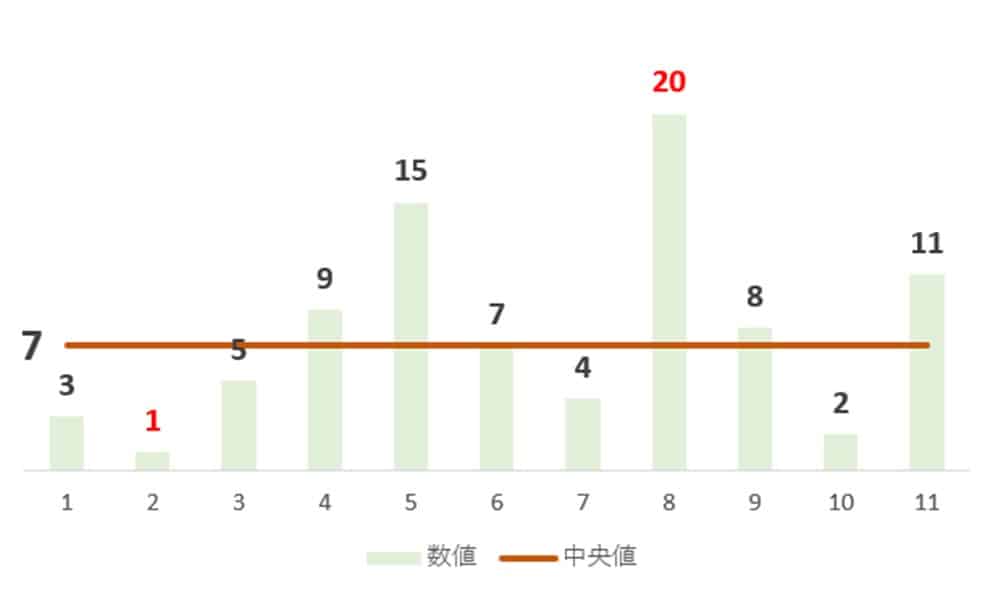
視覚的に異常値をアピールしたい場合に便利です。
以下の表で説明します。
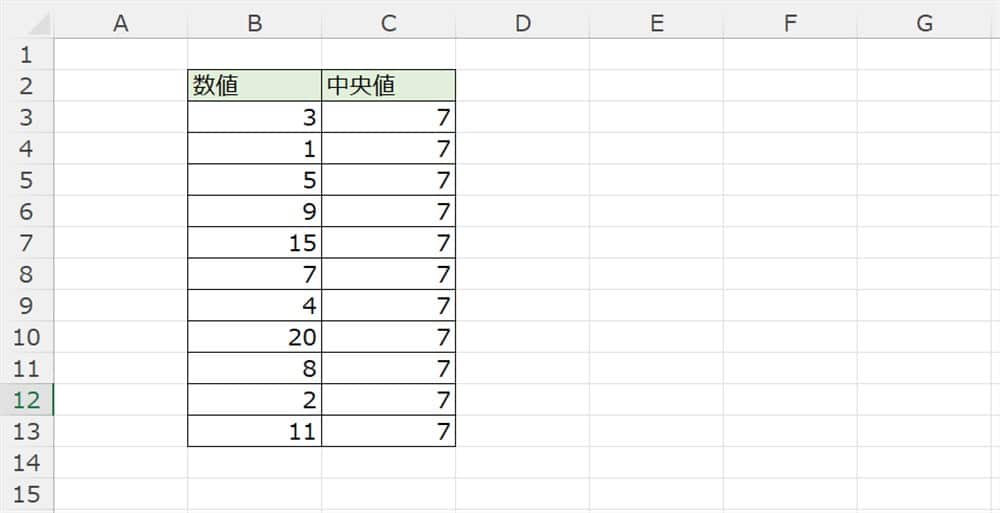
まずはすべての値の右隣にMEDIAN関数を使って中央値を出します。
C3に
と入力して、C13までドラッグすればOKです。
すると下記画像のようになります。
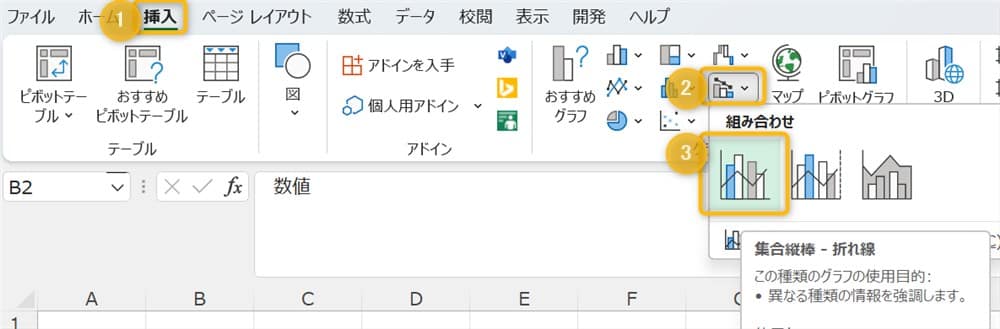
できた表を元に、2軸グラフを作ります。
表全体(B2からC13)を選んだら、挿入→グラフにある組み合わせ→集合縦棒 - 折れ線の順に選びます。
すると、このようになります。
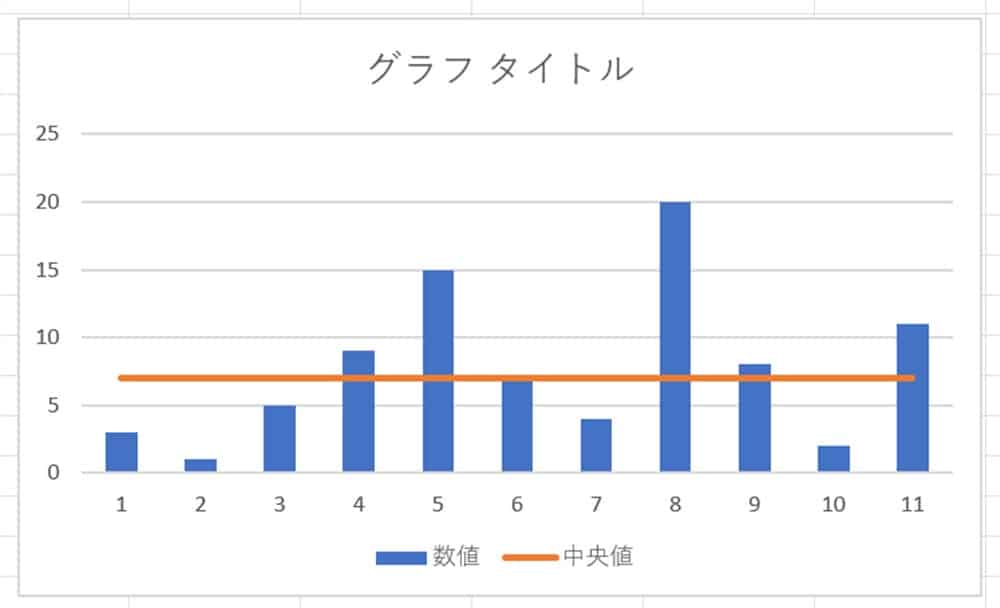
あとは少し装飾してグラフを見やすくしましょう。
これで中央値をグラフに反映できました。
【応用③】箱ひげ図で中央値を含めたデータのばらつきを表す
データごとのばらつきや傾向を比較するには、箱ひげ図を使います。
以下の表を使って、箱ひげ図を出してみましょう。
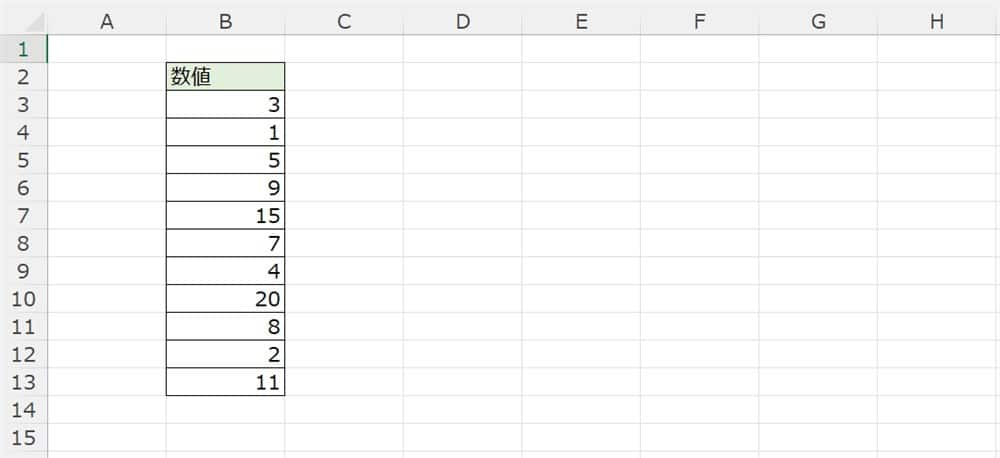
まずはデータ範囲を設定します。
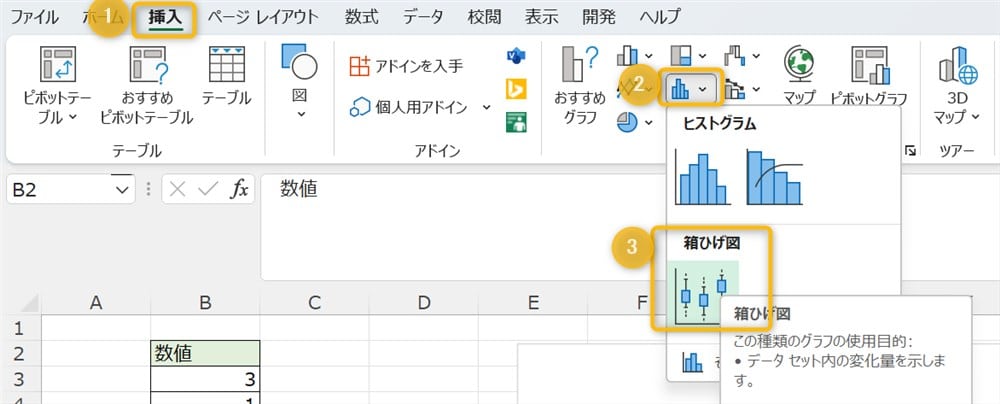
B2からB13を選んだら、挿入→グラフにある統計グラフの挿入→箱ひげ図を選びます。
すると、下記のようなグラフができます。
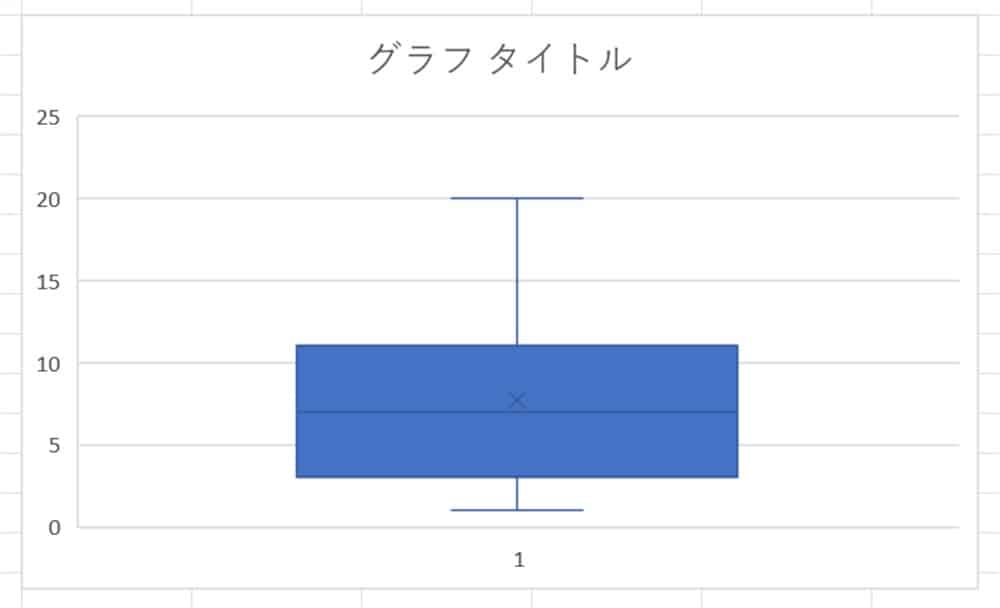
ただ、これでは何がなんだかわかりませんよね……。
そこで、データラベルをつけてみます。
グラフ→+ボタンの順にクリックし、データラベルにチェックをいれましょう。
すると、箱ひげ図にデータラベルが表示されます。
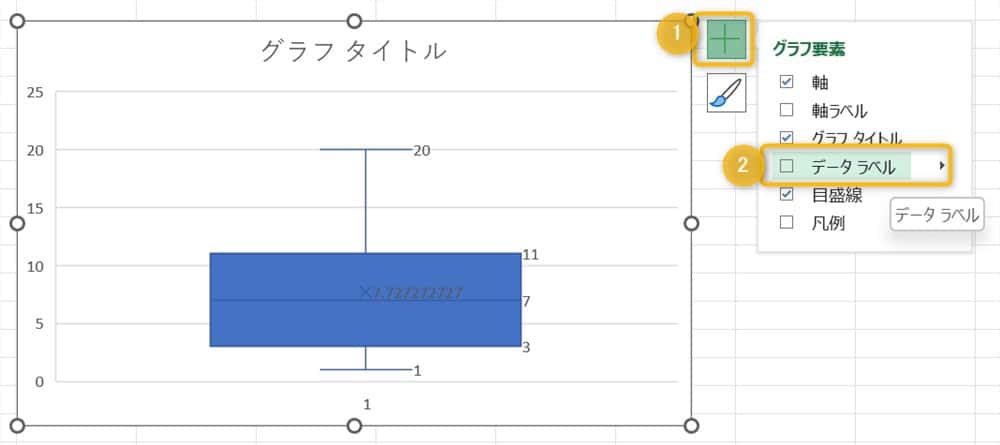
これでもまだわかりにくいので、少し加工しました。
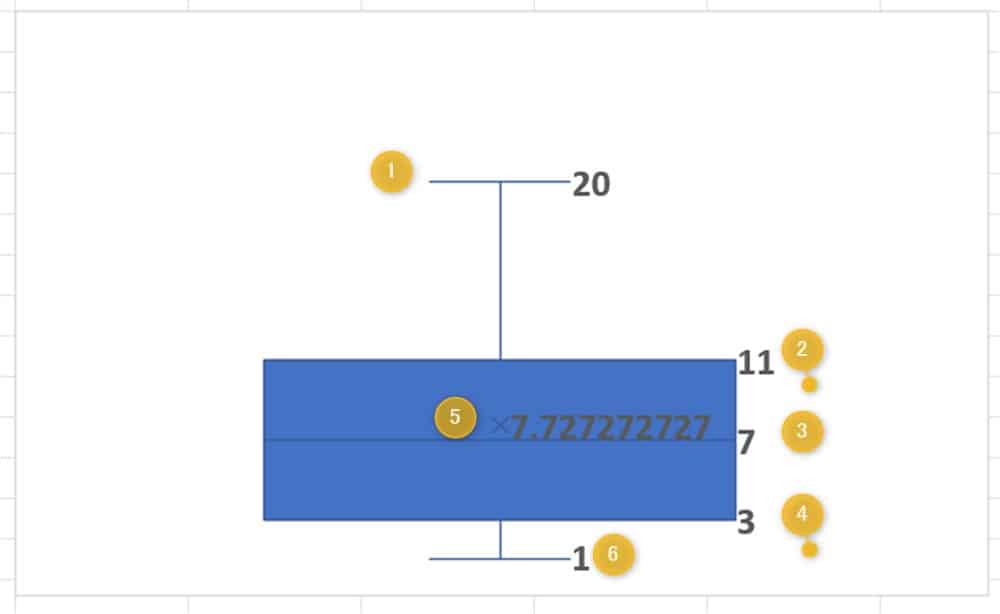
それぞれの数値の説明は下記になります。
- 表内の最大値
- 表内の75%の値(第3四分位数)
- 中央値
- 表内の25%の値(第2四分位数)
- 平均値
- 表内の最小値
箱ひげ図を使えば中央値をすぐに算出できるだけでなく、データのばらつきがどの程度なのかが一目瞭然です。
ぜひ使ってみてください。
まとめ
以上、中央値について解説しました。
中央値は平均値とは違い、異常値の影響を受けずに実態に近い値を出せます。
中央値を出すにはいくつかのステップがありますが、ExcelであればMEDIAN関数を使って算出できます。
また年代別や商品別など、条件をつけて中央値を出したり箱ひげ図などのグラフで視覚的にアピールするのも可能です。
うまく使えばデータ分析に説得性を持たせられるので、ぜひ使ってみてください。





























